Binomial distribution pops up in our problems daily, given that the number of occurrences 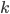of events with probability 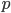in a sequence of size 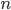can be described as

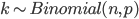
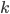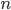Question that naturally arises in this context is - given observations of and , how do we estimate 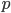? One might say that simply computing 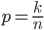should be enough, since that's both uniformly minimum variance and a maximum likelihood estimator. However, such estimator might be misleading when 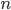is small (as anyone trying to estimate clickthrough rates from small number of impressions can testify).

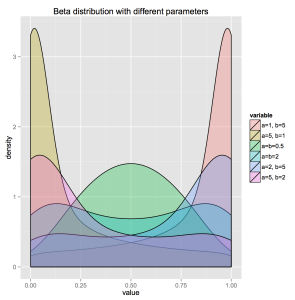
The question is - what can we do ? One thing that naturally comes to mind is incorporating any prior knowledge about the distribution we might have. A wise choice for prior of binomial distribution is usually Beta distribution, not just because of it's convenience (given that it's conjugate prior), but also because of flexibility in incorporating different distribution shapes

In this context, we can express our model as:

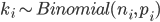
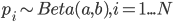
where 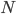is total number of observations an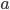d and 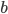are parameters to be estimated. Such model is also called Empirical Bayes. Unlike traditional Bayes, in which we pull prior distribution and it's parameters out of the thin air, Empirical Bayes estimates prior parameters from the data.

In order to estimate parameters of the prior, we calculate marginal distribution as

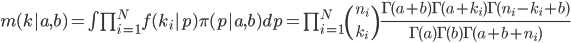
where 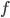and 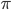are density functions of binomial and beta distributions, respectively. Parameter estimates 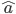and 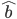can be obtained by maximizing the log likelihood of the marginal distribution.

Finally, Empirical Bayes estimator can be constructed as expectation of posterior distribution:

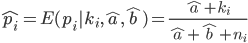
Pretty easy. The real question is - how do we do this in practice ? It turns out that there is no off-the-shelf package in R for doing this, so we have built one. It relies pretty heavily on fitdistrplus package and there are certainly a number of things to be improved, but it's a start. You can grab it at our Github repository.